Download the Product Belief file Here:
BoxMuller Guassion Noise Generator for FPGA v1.0
Now, we have published the Verilog source code and the bit-match verification script on Github. Please go to https://github.com/zhanxn87/awgn_boxmuller
Features
- Based on the Box-Muller algorithm with no central limit theorem required
- Piecewise polynomial based Chebyshev function approximation units with range reduction
- The period of generated noise sequence is 2^88 (about 10^25)
- 18-bit noise samples with 5 bits of integer and 13 bits of fraction, accurate to one unit in the last place (ulp) up to 8.25*sigma, which models the true Gaussian PDF accurately for a simulation size of over samples 10^15
- The core can be reset to its initial state and work on clock enable signal
- Bit-true MATLAB and C mex programs included
- Maximum clock rate and output sample rate of 320MHz on Xilinx VCU108 Board
Box-Muller Algorithm
The Box–Muller transform, by George Edward Pelham Box and Mervin Edgar Muller [1], is a pseudo-random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers.
The Box-Muller method starts with two independent uniform random variables over the interval [0, 1). The following mathematical operations are performed to generate two samples, and, of a Gaussian distribution N(0,1).

Normal Distribution Performance Test
Test Environment
Taus_URNG, seeds are 2846420573 2846420573 2846420573
Taus_URNG, seeds are 912462866 912462866 912462866
Test Generated samples number for analysis: 1e7
Fixed point Accuracy Evaluation
Fixed point output is compared to float point model (with same URNG input):
| Floor truncation | Round | |
| e max error value (abs) | 6.3224e-08 | 3.4341e-08 |
| f max error value (abs) | 3.1588e-05 | 2.3977e-05 |
| g0/g1 max error value (abs) | 1.0174e-04
1.0174 e-04 |
1.1467e-04
1.1467 e-04 |
| x0/x1 max error value (abs) | 4.8891e-04
4.8123e-04 |
5.5051e-04
6.1058e-04 |
| x0/x1 mean value | -5.6479e-04
8.4952e-05 |
-5.6477e-04
8.4947e-05 |
| x0/x1 variance value | 0.99978
1.0001 |
0.99982
1.0001 |
The results show that accuracy loss caused by truncation can be neglected. So truncation method is used in hardware.
Anderson-Darling test result
adtest result (vs. MATLAB randn() function):
| H | P | adsta | cv | |
| This design | 0 | 0.7810 | 0.2398 | 0.7519 |
| MATLAB randn() | 0 | 0.3270 | 0.4209 | 0.7519 |
H=0 means data sets fit the normal distribution.
Distribution Figure

Figure 1. PDF Distribution of generated 1e7 samples
Resource Utilization and Throughput
Xilinx VCU108 FPGA Evaluation Board
Fmax : 330MHz (can be improved furthermore)
Latency : 16 cycles
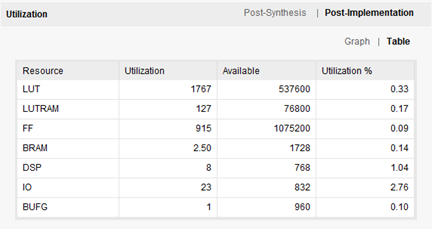
Figure 2. Resource Utilization