BoxMuller AWGN Signal Generator For FPGA (Open Source Verilog)
Acknowledgment
Box-Muller AWGN signal generator implemented for FPGA/ASIC is presented. Mainly refer to [6] and [7], thanks to the authors.
Now, we have published the Verilog source code and the bit-match verification script on github. Please go to https://github.com/zhanxn87/awgn_boxmuller
Features
- Based on the Box-Muller algorithm with no central limit theorem required
- Piecewise polynomial based Chebyshev function approximation units with range reduction
- The period of generated noise sequence is 2^88 (about 10^25)
- 18-bit noise samples with 5 bits of integer and 13 bits of fraction, accurate to one unit in the last place (ulp) up to 8.16*sigma, which models the true Gaussian PDF accurately for a simulation size of over samples 10^15
- The core can be reset to its initial state and work on clock enable signal
- Bit-true MATLAB and C mex programs included
- Maximum clock rate and output sample rate of 320MHz on Xilinx VCU108 Board
Box-Muller Algorithm
The Box–Muller transform, by George Edward Pelham Box and Mervin Edgar Muller [1], is a pseudo-random number sampling method for generating pairs of independent, standard, normally distributed (zero expectation, unit variance) random numbers, given a source of uniformly distributed random numbers.
The Box-Muller method starts with two independent uniform random variables, and, over the interval [0, 1). The following mathematical operations are performed to generate two samples, and, of a Gaussian distribution N(0,1).

Fixed Point Method
Generally, when evaluating channel codes, one needs 100 to 1000 bits in error to draw conclusions on a simulation with enough confidence. Hence, with samples, one can examine channel code behavior for bit error rates as low as 10^-12 to 10^-13.
Two key specifications are set for our noise generator: periodicity of and 16-bit noise samples. In order to meet the periodicity requirement, the URNGs should have a period of at least 10^15.
By examining the normal distribution N(0,1) using norminv function in MATLAB, we observe that we need to be able to represent up to for a population of samples. In other words, the probability of the absolute value of a single sample from that population being larger thanis less than 0.5 (0.444 to be exact).
Bit-width for u0 and u1
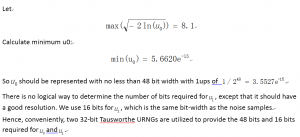
Bit-width for e, f, and g
After generating the two 32-bit Tausworthe URNGs numbers u0 and u1. The implementation of (3)~(5) in hardware utilizes look up tables where the coefficients were found using Chebyshev series approximations [5].
Moreover, function (3) and (4) processing need to split into three steps: range reduction, function approximation and range reconstruction [6][7]. These steps are utilized because it facilitates the implementation by lowering the complexity to only approximating the function on a smaller input interval. Truncation is used here to further decrease hardware complexity.
Chebyshev coefficients for (3) (4) and (5) approximation are generated with MATLAB codes, refer to “chebv_approx.m” file. For example, the Degree-2 Chebyshev approximation coefficients for –ln(x) calculation is like this:
The error analysis starts at the end and makes its way back to the beginning because the main goal is for the output’s error to meet the faithful rounding requirement. Please refer to [6] and [7] for detailed analysis descriptions. The result of fixed point from [6] is as Figure 1 (f and g width expanded).
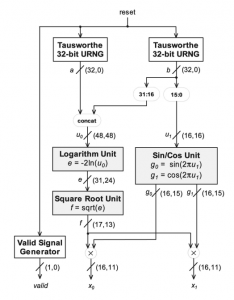
Figure 1 Hardware Computation procedure diagram from [6]
Hardware Implementation
Tausworthe URNG Generation
Although traditional linear feedback shift registers (LFSRs) are often sufficient as a uniform random number generator (URNG), Tausworthe URNGs [3] are fast and occupy less area. Tausworthe URNG follows the algorithm presented by L’Ecuyer [4], which combines three LFSR-based URNGs to obtain improved statistical properties. It generates a 32-bit uniform random number per clock and has a large period of (about).
Figure 2 Tausworthe URNG generation codes
Normal Distribution Performance Test
Test Environment
Taus_URNG, seeds are 2846420573 2846420573 2846420573
Taus_URNG, seeds are 912462866 912462866 912462866
Test Generated samples number for analysis: 1e7
Fixed point Accuracy Evaluation
Fixed point output is compared to float point model (with same URNG input):
| Floor truncation | Round | |
| e max error value (abs) | 6.3224e-08 | 3.4341e-08 |
| f max error value (abs) | 3.1588e-05 | 2.3977e-05 |
| g0/g1 max error value (abs) | 1.0174e-04
1.0174 e-04 |
1.1467e-04
1.1467 e-04 |
| x0/x1 max error value (abs) | 4.8891e-04
4.8123e-04 |
5.5051e-04
6.1058e-04 |
| x0/x1 mean value | -5.6479e-04
8.4952e-05 |
-5.6477e-04
8.4947e-05 |
| x0/x1 variance value | 0.99978
1.0001 |
0.99982
1.0001 |
The results show that accuracy loss caused by truncation can be neglected. So truncation method is used in hardware.
Anderson-Darling test result
adtest result (vs. MATLAB randn() function):
| H | P | adsta | cv | |
| This design | 0 | 0.7810 | 0.2398 | 0.7519 |
| MATLAB randn() | 0 | 0.3270 | 0.4209 | 0.7519 |
Distribution Figure
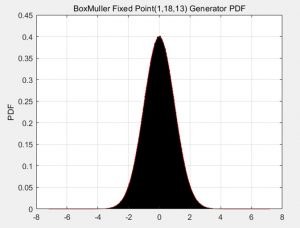
Figure 3. PDF Distribution of generated 1e7 samples
Resource Utilization and Throughput
Xilinx VCU108 FPGA Evaluation Board
Fmax : 330MHz (can be improved further more)
Latency : 16 cycles
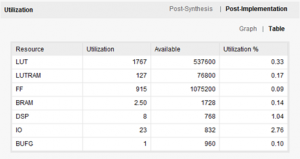
Figure 4. Resource Utilization
More Methods to generate AWGN
Wallace method
D.-U. Lee, W. Luk, J. D. Villasenor, G. Zhang, and P. H. W. Leong, “A hardware gaussian noise generator using the wallace method,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 13, no. 8, pp. 911–920, Aug 2005.
Ziggurat methods
Hörmann and J. Leydold, “Continuous random variate generation by fast numerical inversion,” ACM Trans. Model. Comput. Simul., vol. 13, no. 4, pp.347–362, Oct. 2003
Inversion method
Gutierrez, V. Torres, and J. Valls, “Hardware architecture of a gaussian noise generator based on the inversion method,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 59, no. 8, pp. 501–505, Aug 2012.
C. C. Cheung, D. U. Lee, W. Luk, and J. D. Villasenor, “Hardware generation of arbitrary random number distributions from uniform distributions via the inversion method,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 15, no. 8, pp. 952–962, Aug 2007.
CORDIC use
S. Malik, A. Hemani, and N. D. Gohar, “Unifying cordic and box-muller algorithms: An accurate and efficient gaussian random number generator,” in 2013 IEEE 24th International Conference on Application-Specific Systems, Architectures and Processors, June 2013, pp. 277–280.
Wang and Z. Bie, “A novel hardware gaussian noise generator using box-muller and CORDIC,” in 2014 Sixth International Conference on Wireless Communications and Signal Processing (WCSP), Oct 2014, pp. 1–6.
Reference
[1] G. E. P. Box and Mervin E. Muller, A Note on the Generation of Random Normal Deviates, The Annals of Mathematical Statistics (1958), Vol. 29, No. 2 pp. 610–611 doi:10.1214/aoms/1177706645, JSTOR 2237361
[2] Box-Muller Transform wiki page https://en.wikipedia.org/wiki/Box%E2%80%93Muller_transform#cite_note-1
[3] R.C. Tausworthe, “Random Numbers Generated by Linear Recurrence Modulo Two,” Math. and Computation, vol. 19, pp. 201-209, 1965.
[4] P. L’Ecuyer, “Maximally Equidistributed Combined Tausworthe Generators,” Math. Computation, vol. 65, no. 213, pp. 203-213, 1996.
[5] M. J. Schulte and E. E. Swartzlander, “Hardware designs for exactly rounded elementary functions,” IEEE Transactions on Computers, vol. 43, no. 8, pp. 964–973,Aug 1994.
[6] D. U. Lee, J. D. Villasenor, W. Luk, and P. H. W. Leong, “A hardware Gaussian noise generator using the box-muller method and its error analysis,” IEEE Transactions on Computers, vol. 55, no. 6, pp. 659–671, June 2006.
[7] Lincoln Glauser, “The Design of a 24-bit Hardware Gaussian Noise Generator via the Box-Muller Method and its Error Analysis”, (2017). Tesis. Rochester Institute of Technology.
Comment (1)
http://canadianorderpharmacy.com/| June 3, 2019
Excellent pieces. Keep writing such kind of info on your blog. Im really impressed by your blog.
Hi there, You have done a great job. I will certainly digg it and individually recommend to my friends. I’m confident they’ll be benefited from this web site.